Figure 2-6.—"Stepping off" with a framing square.
the tongue and the blade even with the edge of the board.
Draw the pencil marks as shown. The distance between
these marks, measured along the edge of the board, is
the length of the hypotenuse of a right triangle with the
other sides each 12 inches long. You will find that the
distance, called the bridge measure, measures just under
17 inches—16.97 inches, as shown in the figure. For
most practical Builder purposes, though, round 16.97
inches to 17 inches.
Solving for Unit and Total Run and Rise
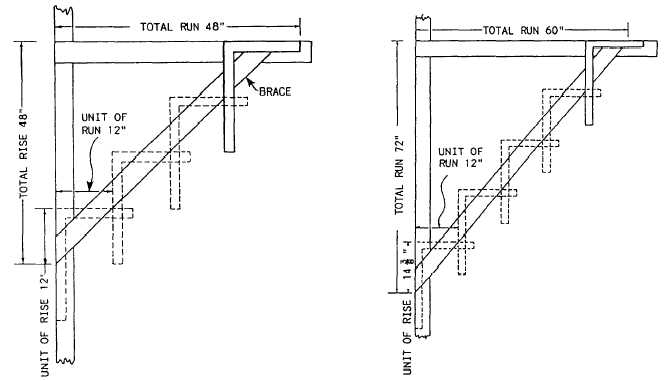
In figure 2-5, the problem could be solved by a
single set (called a cut) of the framing square. This was
due to the dimensions of the triangle in question lying
within the dimensions of the square. Suppose, though,
you are trying to find the length of the hypotenuse of a
right triangle with the two known sides each being 48
inches long. Assume the member whose length you are
trying to determine is the brace shown in figure 2-6. The
total run of this brace is 48 inches, and the total rise is
also 48 inches.
To figure the length of the brace, you first reduce
the triangle in question to a similar triangle within the
dimensions of the framing square. The length of the
vertical side of this triangle is called unit of rise, and the
length of the horizontal side is called the unit of run. By
Figure 2-7.–"Stepping off" with a square when the unit of run
and unit of rise are different.
a general custom of the trade, unit of run is always taken
as 12 inches and measured on the tongue of the framing
square.
Now, if the total run is 48 inches, the total rise is 48
inches, and the unit of run is 12 inches, what is the unit
of rise? Well, since the sides of similar triangles are
proportional, the unit of rise must be the value of x in
the proportional equation 48:48::12:x. In this case, the
unit of rise is obviously 12 inches.
To get the length of the brace, set the framing square
to the unit of run (12 inches) on the tongue and to the
unit of rise (also 12 inches) on the blade, as shown in
figure 2-6. Then, “step off” this cut as many times as the
unit of run goes into the total run. In this case, 48/12, or
4 times, as shown in the figure.
In this problem, the total run and total rise were the
same, from which it followed that the unit of run and
unit of rise were also the same. Suppose now that you
want to know the length of a brace with a total run of 60
inches and a total rise of 72 inches, as in figure 2-7. Since
the unit of run is 12 inches, the unit of rise must be the
value of x in the proportional equation 60:72::12.x. That
is, the proportion 60:72 is the same as the proportion
12:x. Working this out, you find the unit of rise is
2-5